The well-known formula for the efficiency of an ideal Carnot engine is
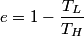 where 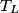 is the temperature of the low-temperature reservoir and is the temperature of the low-temperature reservoir and 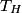 is the temperature of the high-temperature reservoir (see page 522 of Giancoli). Both temperatures MUST be in Kelvin. The efficiency is DEFINED as is the temperature of the high-temperature reservoir (see page 522 of Giancoli). Both temperatures MUST be in Kelvin. The efficiency is DEFINED as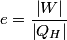 where 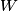 is the work performed by the engine and is the work performed by the engine and 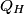 is the heat absorbed from the high-temperature body (see Giancoli page 519). Therefore, if is the heat absorbed from the high-temperature body (see Giancoli page 519). Therefore, if 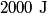 are input into the engine, then the amount of work that the engine performs is are input into the engine, then the amount of work that the engine performs is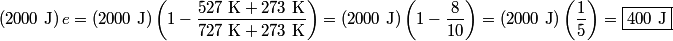 Therefore, answer (A) is correct. |